Exatas assusta muita gente. Integrais, derivadas e limites. Quem pretende se formar em engenharia e em carreiras da área de exatas, precisa lidar com estes e outros conceitos do cálculo.
A disciplina de cálculo permitiu descobertas na química, na física, na matemática, na astronomia, na biologia, na economia e em diversas outras áreas.
O conteúdo é fundamental para futuros engenheiros, como analisa o coordenador de Conteúdo do Responde Aí, Jorge Alberto Santos. “Os alunos estão se preparando para lidar com problemas e conseguir criar soluções.
Algumas questões comuns na vida de um engenheiro são, por exemplo, calcular a área de superfícies, volume de objetos, calcular a taxa de crescimento de determinada população ou até mesmo a taxa de transmissão de um vírus.
Para resolvê-las, é necessário entender as principais operações do cálculo, que são os limites, as derivadas e as integrais.” É uma das áreas indispensáveis da educação.
Desenvolvido por Isaac Newton a partir da álgebra e da geometria, o cálculo estuda a variação de grandezas e o acúmulo de quantidades.
Além disso, ajuda a resolver problemas em que há movimento ou crescimento, onde forças variáveis agem.
Para o entendimento da disciplina, o ideal é abandonar a decoreba. Os estudantes devem compreender o cálculo, o que significa dedicação e muitos exercícios para estabelecer uma base sólida para outras disciplinas do curso.
Ponto de partida das Exatas
Universitários de Exatas percebem logo no ingresso que entender os conceitos de limites, derivadas e integrais é vital para resolver problemas na disciplina.
“Esses são três assuntos super importantes que formam as bases de todo o cálculo, matéria que estuda as taxas de variação de grandezas e acumulação de quantidades.
Esses tópicos são tão relevantes que a disciplina também é conhecida como Cálculo Diferencial e Integral”, aponta Santos.
O limite é usado para descrever o comportamento de funções, especialmente aquelas que não apresentam interrupções.
Já a integral permite o cálculo da área de uma região curva não simétrica, de uma velocidade não constante, de volumes, além de ter aplicações na física e na biologia.
As derivadas estão relacionadas ao cálculo de uma taxa de variação e dos máximos e mínimos de uma função.
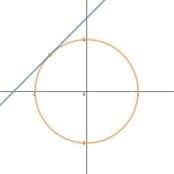
“Através do conceito de derivadas é possível, por exemplo, encontrar a equação da reta tangente em uma curva. Na circunferência [na imagem acima], a reta tangente é aquela que se aproxima do círculo, encosta nele em apenas um ponto, e passa a se afastar dele.
Para encontrar a equação dessa reta, é necessário entender o conceito de derivadas”, explica o coordenador de Conteúdo do Responde Aí.
Evitando o tabu das Exatas
Não faltam relatos de estudantes que perdem o sono e sofrem quando se deparam com a disciplina. Para muitos, o cálculo torna-se um tabu. A orientação de Jorge Alberto Santos é evitar que ocorra um processo desfavorável ao aprendizado.
“A melhor forma de criar motivação para estudar e aprender algo novo, é entender a razão de se estudar determinado assunto.
Quando o aluno entende o porquê das coisas, o estudo fica muito mais leve, porque fica claro aonde se quer chegar e quais são as aplicações práticas da matéria.
Na vida de um estudante de engenharia, não é diferente: entender o objetivo de cada aula ou conceito novo pode ajudar bastante a superar o medo ou o bloqueio.”
Atividades práticas ajudam
A prática é fundamental. Não basta ficar apenas na teoria, na sala de aula ou em complementos em videoaulas.
É preciso resolver a maior quantidade de exercícios possível, seja de livros, de lista do professor, de provas antigas ou de sites especializados.
À medida que sentir que está evoluindo, o estudante deve aumentar o nível das questões, das mais simples às mais complexas, pode por exemplo receber explicações de álgebra linear.
Como os problemas costumam ter uma base parecida, o aluno fica mais confiante quando chegarem as provas.
Estar em um meio que permita solucionar problemas reais também ajuda o futuro profissional.
“Uma dica é procurar atividades e projetos fora de sala de aula, onde seja possível aplicar esses conceitos, seja uma extensão na faculdade, iniciação científica ou estágio”, orienta Jorge Alberto Santos.
Texto sobre Exatas escrito por: Rodolfo Milone

